Здесь я пошагово разбираю создание игры от основ языка C# до компиляции вашего проекта под windows, android и web.
Ссылка на книгу: https://www.litres.ru/71838403/
Авторский блог связанный с обучением программированию, точным наукам и робототехнике всех желающих от детского возраста до старческого возраста
Эта книга, в первую очередь, нацелена на помощь начинающим роботехникам погрузиться в мир сборки, проектирования и программирования электронных устройств. За основу были взяты платы семейства Arduino. Они общедоступны и универсальны для многих задач.
Самые трудные моменты в робототехнике это:
Есть подробное описание использования того или иного измерительного прибора и инструмента для крепления и монтажа.
Многие главы снабжены ссылками на видеоуроки, поясняющие данную тему или показывающие пработу на практике. Это поможет читателю исключить многие ошибки.
Примеры устройств:
1. Сейф с кодовым замком
2. Мобильный робот
3. светодиодный куб
И многое другое.
You can also use mBlock 5 on the web without downloading it.
mBlock 5 webpage: https://ide.mblock.cc
To connect a device to mBlock 5 on the webpage, you need to install mLink first.
PC system:Windows 7 or later (64-bit systems recommended); macOS 10.10 or later; 64-bit Linux
Browser: Chrome recommended
mBlock 5 webpage: https://ide.mblock.cc
Devices supported: Bluetooth Controller, Codey Rocky, HaloCode, mBot, MotionBlock, Neuron, mBot Ranger, Ultimate 2.0, Arduino Uno, Arduino Mega2560, Nova Pi, MegaPi Pro
1. Download mLink.
mLink-Windows installation package
2. Open the installation file and follow the installation wizard.



3. After the installation is complete, the mLink icon is displayed on the desktop and the toolbar in lower right corner.


1. Download mLink.
mLink-macOS installation package
2. Open the installation file and follow the installation wizard.


3. After the installation is complete, the mLink icon is displayed on the launchpad and the taskbar in the upper right corner.


1. Click OK.

2. Choose System Preferences > Security & Privacy.

3. Click Open Anyway.

4. Start the mLink installation process.

1. Right-click the installation package and choose Open.

2. Click Open.
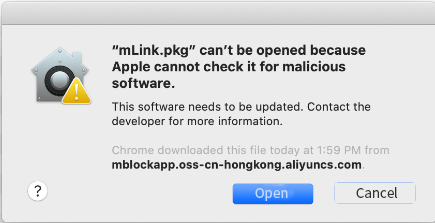
3. Start the mLink installation process.

1. Download mLink.
Red Hat, Fedora, SUSE, CentOS: .rpm installation package
Debian, Ubuntu: .deb installation package
2. Install mLink through command lines.
Install .rpm on Red Hat, Fedora, SUSE, CentOS
(1) Open Terminal, enter the following command, and press Enter:
sudo rpm -ivh --force mLink-1.2.0-1.el7.x86_64.rpm

(2) Enter the following command to start the program:
sudo mblock-mlink start
Enter the following command to stop the program:
sudo mblock-mlink stop
Install .deb on Debian and Ubuntu
(1) Open Terminal, enter the following command, and press Enter:
sudo dpkg -i mLink-1.2.0-amd64.deb

(2) Enter the following command to start the program:
sudo mblock-mlink start
Enter the following command to stop the program:
sudo mblock-mlink stop
Ниже представлено содержание книги.
Математические приключения в игре Minecraft с Python
Авторы: Корягин Андрей Владимирович
Корягина Алиса Витальевна
Элементарные математические функции
Основы математики были описаны в первой книге «Python. Великое программирование в Minecraft». К данным основам относятся знания в области математических операторов, операторов сравнения, основ теории чисел (целые и дробные). На этом познания в математике не заканчиваются, и дальше, согласно школь-
ной программе, идут решения уравнений и неравенств и различных систем из них, которые перерастают в изучение функций и построение графиков. Затем идёт усложнение уравнений и функций. Все эти моменты мы постараемся рассмотреть в данной книге.
Для упрощения написания программ,связанных с математикой, для разных языков программирования разрабатывались математические библиотеки. Для языка Python — это библиотека math.
Математические приключения в игре Minecraft с Python
2.1. Библиотека math
Модуль math в Python предоставляет набор функций для выполнения математических, тригонометрических и логарифмических операций. Некоторые из основных функций модуля:
ƒ pow(num, power): возведение числа num в степень power
ƒ sqrt(num): квадратный корень числа num
ƒ ceil(num): округление числа до ближайшего наибольшего
целого
ƒ floor(num): округление числа до ближайшего наименьшего
целого
ƒ factorial(num): факториал числа
ƒ degrees(rad): перевод из радиан в градусы
ƒ radians(grad): перевод из градусов в радианы
ƒ cos(rad): косинус угла в радианах
ƒ sin(rad): синус угла в радианах
ƒ tan(rad): тангенс угла в радианах
ƒ acos(rad): арккосинус угла в радианах
ƒ asin(rad): арксинус угла в радианах
ƒ atan(rad): арктангенс угла в радианах
ƒ log(n, base): логарифм числа n по основанию base
ƒ log10(n): десятичный логарифм числа n
ƒ math.hypot(X, Y): вычисляет гипотенузу треугольника с кате-
тами X и Y (math.sqrt(x * x + y * y))
ƒ math.pi: константа pi = 3,1415926…
ƒ math.e: константа e = 2,718281…
Данная библиотека содержит стандартный набор функций,которые непосредственно применяют школьники с 1 по 11 класс, с затрагиванием и вузовского материала. Со всеми функциями math мы не будем знакомиться, для этого есть документации к библиотекам и книги о детальном их разборе. В первую очередь рассмотрим функции, которые встречаются в школьной программе, и постараемся связать математическую запись с решением практических задач. Начнём с изучения линейных функций общего вида
y = k * x + b.
2.2. Линейные функции и их графики
Линейными функциями называют функции вида y = k * x, где k —это угловой коэффициент или коэффициент пропорциональности. В учебниках по математике существует такая запись: y = k * x + b, где k — это угловой коэффициент или коэффициент пропорциональности, b — число из множества рациональных или иррациональных чисел.
Данную функцию принято называть в профессиональном кругу математиков «аффинной», но в школьных учебниках её называют «линейной». Значение k влияет на то, как будет строиться график, — под каким
углом относительно оси X и Y он будет проходить.
Элемент b указывает на то, где график пересечётся с осью, если x = 0.
Есть два вида задач для этих функций:
ƒ нахождение k и b, если известны точки, принадлежащие графику;
ƒ проверить на принадлежность к графику точек с определёнными координатами.
Звучит вроде страшно и непонятно. Выйдем из абстракции к реальному миру. Возьмите длинную прямую палку, можно заменить на линейку. Палка также описывается данной функцией, в зависимости от того, как мы её расположим относительно начала координат. Что такое начало координат в физическом мире?
Началом координат в реальности может выступить всё что угодно, в основном что-то неподвижное: дерево, стул, стакан, дом, камень… Всё будет зависеть от того, какого размера вы возьмёте палку и какую точность измерения хотите получить. В седьмом классе очень много задач в геометрии и физике на нахождение
размеров объекта и определение расстояния между предметами, и подход с использованием функций также применим к ним.
«Зачем это нужно?» — спросите вы. На это есть множество обоснований, начнём с простого. Вы играете в футбол или стреляетев тире. В обоих случаях ваша задача — попасть в цель. Вы стараетесь бить по прямой, так чтобы мяч или пуля перемещалась вдоль представленного графика линейной функции. Этот график прохо-
дит через ворота или цель в мишени, т. е. координаты этих объектов принадлежат графику линейной функции или, иными словами, траектории движения.
Конечно, в данном случае никто из нас в юном возрасте не начнёт выписывать в этот же момент функцию
и вычислять правильную позицию, всё делается «на глаз», как нам кажется, но мозг всё это просчитывал за доли секунды, и воображаемая траектория полёта мяча — это тоже работа вашего мозга, который соединил две точки и провёл неосознанные вычисления.
Вроде как не убедительный пример применения данных знаний, но опытные игроки так и поступают — создают план действий и набрасывают траекторию движений. Рассмотрим более современный вариант, когда вы непосредственно не видите конечной цели. Например, это запуск спутников и ракет, симулятор стрельбы в компьютерных играх, разработка программного обеспечения для беспилотного транспорта… Во всех этих примерах во время их реальной работы ваше участие сводится к минимуму.
Вычислением и построением графиков функций траектории движения транспорта занимаются исключительно компьютеры.
И от того, как правильно вы определили функцию и подобрали коэффициенты, будет зависеть результат процесса. Во всех этих случаях машина должна просчитать координаты двух точек в определённый момент времени, построить график, проходящий через них, запустить процесс (запуск ракеты, полёт пули, движение в определённом направлении согласно условию) и отслеживать координаты полёта или движения с течением времени, чтобы создать отчёт о проценте успеха реализации задачи.
Теперь немного становится ясно, что математика нужна для получения точного и красивого результата, а не «на глаз». Для решения многих современных задач требуется большая точность, и здесь без математики не обойтись. Но вернёмся к линейным функциям. Сейчас мы попробуем построить графики функций
в Minecraft с разными значениями k и b, чтобы увидеть наглядно, как они влияют на построение.
Для визуализации графиков нам понадобится среда Minecraft, знания в области Minecraft API и Python. Строить графики будем по точкам, т. е. по блокам. Поэтому нам необходима функция setBlock() (смотри приложение).
Рассмотрим первый столбец таблицы и построим для каждой функции графики в Minecraft. Чтобы
различать графики, будем использовать блок «шерсть» с разным цветом (смотри приложение).
Создадим файл lin1.py и запишем стандартные строки кода для импортирования библиотеки Minecraft и настройки связи между кодом и игрой. Импортируем библиотеку по работе с блоками Minecraft и вызовем функцию получения координат игрока (более подробно рассматривается в книге «Python. Великое программи-
рование в Minecraft»).
Для того чтобы запись координат была приведена к общеизвестному виду, создадим переменные x, y, z и присвоим им значения координат игрока.
Рассмотрим первую функцию: y = 0.
Графиком этой функции является прямая, параллельная оси X, т. е. все точки графика будут
находиться на одном расстоянии от оси X. Точнее, прямая будет совпадать с осью X, потому что при любом значении x переменная y принимает значение, равное нулю.
Как это можно реализовать программно? Для этого воспользуемся конечным циклом.
Хоть и прямая бесконечная, но она в любой точке будет неизменной, поэтому достаточно взять отрезок. Возьмём участок графика в промежутке x ∈ [0, 20), т. е. размер прямой будет 20 блоков от позиции игрока.
Для этого графика возьмём белую шерсть.
Выражение: y1 = 0 * x + 0 равносильно функции y = 0, где k = 0 и b = 0.
С каждым шагом мы строим блок, сдвигаясь по оси X на один блок, при этом значение y не меняется, согласно математической записи функции.
Программу необходимо сохранитьв Minecraft Python Minecraft Tools MinecraftPythonAPI
py3minepi-master.
Результат программы представлен на рис. 28.
Теперь, по аналогии, построим остальные графики.
Начнём с y = 0.2 * x.
Для неё запишем аналогичный код и покрасим шерсть в оранжевый цвет:
Запустим программу и получим результат, как на рис. 29.
Как видно, вместо ожидаемой прямой линии представлена ломаная. Это связано с масштабом построения и погрешностью. Так как мы взяли малый промежуток отрезка, а точка графика равна 1/20 размера от целого блока, и блоки в среде строятся по целым значениям, т. е. половина блока строиться не будет, то получаем
соответствующий график. Если увеличить промежуток до 100, то с расстоянием эта кривая «выпрямляется».
Напишем для всех остальных функций коды, где k ≥ 0:
Результат работы программы изображён на рис. 30.
Таким же свойством обладает тригонометрическая функция (тангенс) - tg(a), при tg(90°) = ∞.
Поэтому принято считать что, k = tg(a).
Но график, который перпендикулярен оси X, существует. Его математическая запись принимает вид:
x = 0 или x = b. Постройте такой график самостоятельно.
Для примера связи k с tg(a) построим график функции y = x, где k = 1.
Из геометрии известно, что tg(a) равен отношению противолежащего катета к прилежащему в прямоугольном треугольнике.
В данном случае tg(a) = 1.
Открыв таблицу Брадиса, можно легко найти, что tg(a) = 1 при a = 45°.
Построим данный график функции с использованием tg(a).
Для того чтобы применить правильно тригонометрические функции,необходимо учесть то, что в языке программирования Python используется значение угла не в градусах, а в радианах.
Существует общая формула перевода градусов в радианы:
Для вызова тригонометрических функций и числа pi используют библиотеку math. Создадим файл lin2.py и импортируем библиотеки:
Теперь осталось написать код для подключения к креативному миру, преобразовать для простоты работы координаты и создать цикл на 20 повторений с использованием тригонометрической функции tg(45°).
Как видно, есть несколько нюансов записи кода:
ƒ в учебниках по математике принято писать tg, а во многих языках программирования tan;
ƒ угол записан в формате формулы для перевода градусной меры в радианную, и чтобы значение было наиболее точное,вызывают число pi из библиотеки math.
Результат работы программы представлен на рис. 31.
Для сравнения вы можете запустить обе программы и убедиться, что графики функции y = x строятся одинаково, так как 1 — точ-
ное значение.
Если вы будете брать нецелые значения k, то припостроении более длинного графика возможны незначительные
отклонения.
В первую очередь это связано с округлением в средеMinecraft.
Осталось для анализа построить графики функций с k < 0. Для этого рекомендуем подняться в воздух в среде Minecraft (по умолчанию — двойное нажатие клавиши ПРОБЕЛ).
Добавим в программу lin1.py код с отрицательными значениями k<0:
Если запустить программу, то мы получим результат, изобржённый на рис. 32.
Как видно, если k < 0, то график функции направлен вниз и симметричен графикам с равным по модулю k.
Некоторые читатели спросят: «А что такое модуль?»
Модуль — это некий математический оператор, который выводит только положительное значение числа при любом его значении. Общая запись модуля: |a| = |–a| = a.
В нашем случае график функции y = x симметричен графику функции y = –x, а y = 1.5 * x симметричен
y = –1.5 * x и т. д.
Мы рассмотрели построение графиков функций только с положительными значениями x, но также можно рассматривать и отрицательные значения.
Создадим файл lin3.py и скопируем весь код из файла lin1.py.
Изменим в каждом цикле диапазон с [0, 20) до [–20, 20).
Полный код представлен ниже:
Теперь рассмотрим графики функций, при которых k = 0, а b ≠ 0.
Создадим файл lin4.py. Импортируем нужные библиотеки для Minecraft и оптимизируем вывод координат:
Создадим код по уже ранее известной схеме для построения нужных графиков:
Код для построения графиков такой же, как и в предыдущих программах, за исключением небольшого нюанса для корня из 12.
Для того чтобы извлекать корни, необходима функция. Во многих языках программирования корень извлекается с помощью функции sqrt().
Результат представлен на рис. 34.

Как видно, все графики строятся параллельно оси X и проходят точки y, равные 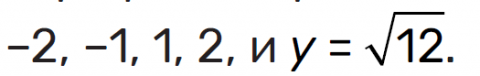
В первой книге «Python. Великое программирование в Minecraft» были похожие построения, когда рассматривалось создание рядов блоков с помощью циклов и отступов по осям X, Y и Z.
Любые фигуры можно строить, непосредственно зная координаты каждой точки, или применять функции, описывающие фигуры. Данные графики функций c k ≠ 0 или b ≠ 0 рассматривались в вышеупомянутой книге.
Для полного понимания применения линейных функций осталось научиться строить графики, где k ≠ 0 и b ≠ 0. Чтобы анализ был намного глубже, предлагаем построить графики с симметричными коэффициентами.
y = –0.5 * x – 10, y = –0.5 * x + 10, y = 0.5 * x – 10, y = 0.5 * x + 10.
Создадим файл с именем lin5.py и импортируем нужные модули для работы с Minecraft:
Далее по аналогии с предыдущими программами создадим четыре цикла:
Как видно, эти четыре графика образовали греческую букву «сигма». Таким знаком в математике обозначают сумму. Для лучшего восприятия рекомендуем построить оси системы координат. Для этого необходимо написать ещё два цикла:
Теперь более наглядно видно, что графики имеют некоторые общие зависимости.
Графики, согласно программе, строятся в таком порядке: первая функция — это белый график, вторая — оранжевый, третья — фиолетовый и четвёртая — бирюзовый.
###############################################################
На этом демонстрационную часть я закончу.
Буду рад узнать ваше мнение. Интересен опыт применения Minecraft или подобных сред в образовании.
Дорогие друзья, вышла книга по разработке 3D игры на Unity моего авторства. Здесь я пошагово разбираю создание игры от основ языка C# до ком...
